C'est la formule qui était publiée dans l'agenda FSE jusqu'en 1988. Avec cette formule simplifiée on peut retrouver le tableau qui apparaissait sur l'agenda FSE jusqu'en 1989.
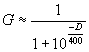
où D est la différence de points Elo entre le joueur et son adversaire.
C'est le calcul actuellement utilisé par la FIDE. Ce calcul repose sur une formule simplifiée, qui donne des résultats approximatifs.
Prenons le cas d'un joueur qui vaut
1600 Elo.
Il joue deux parties contre deux joueurs
de 1600 Elo également et fait deux matchs nuls.
Après ces deux parties, sa performance
actuelle (exacte ou classique) est évidemment de 1600 Elo.
Maintenant ce joueur joue une troisième
partie contre contre Kasparov (2800 Elo) et perd.
Du fait qu'il perd, on s'attend à ce que sa performance diminue légèrement en dessous de 1600 Elo (même très légèrement, puisque Kasparov est beaucoup plus fort).
Sa performance "classique" est :
1/3 = 33% contre une moyenne d'adversaires de 2000 Elo donne une performance de 1880 Elo.
C'est absurde.
Vous pouvez maintenant faire le test suivant avec la Calculette Elo :
Elo de départ : 1880
Elo adversaire 1 : 1600 Rés:
½
Elo adversaire 2 : 1600 Rés:
½
Elo adversaire 3 : 2800 Rés:
0
Résultat : un joueur de 1880 Elo perdrait 16.3 Elo (avec un coeff. de 24) s'il faisait ces résultats. Cela montre encore que le chiffre de 1880 est largement surévalué.
L'erreur est facile à expliquer: il est erroné de se baser sur la moyenne Elo des adversaires. Imaginez que vous jouez contre un joueur avec 10000 Elo: le simple fait de jouer contre lui (peu importe le résultat) fait exploser votre moyenne Elo des adversaires et ainsi votre performance.
Le niveau moyen des adversaires et le score réalisés, ne permettent pas seuls de déterminer le niveau d'un joueur.
Lorsqu'on perd contre un joueur beaucoup plus fort ou on gagne contre un joueur beaucoup plus faible, ce résultat ne renseigne pas beaucoup sur notre niveau et n'a pas un grand impact sur la performance globale.
Pourtant, si on raisonne "moyenne", ce résultat est considéré au même tarif que les autres.
L'erreur de la méthode "classique" peut donc être d'autant plus grande que l'écart entre le niveau du joueur mesuré et ses adversaires est grand.
Lorsqu'un joueur réalise 100% ou 0% des points une autre question se pose: nous ne pouvons pas connaître le niveau de ce joueur. S'il a perdu toutes ses parties, il est clair qu'il doit être considéré plus faible que l'ensemble des adversaires qu'il a rencontrés, mais de combien ?
Là, les fédérations, qui, au bout d'un certain nombre de parties, désirent tout de même introduire les joueurs dans les listes de classement, ont opté pour une méthode heuristique. Dans ces cas, elles ajoutent à la liste de parties, une partie de plus, à considérer comme un match nul contre un joueur de niveau égal à la moyenne des adversaires.
Bien sûr c'est arbitraire, mais
ça permet au moins d'introduire les joueurs à un niveau "raisonnable".
Le gain Elo
Pour calculer le gain Elo, il faut d'abord calculer la chance statistique de gain (résultat escompté) G qui a une valeur en 0 et 1.
Il existent deux méthodes:
C'est la formule qui était publiée dans l'agenda FSE jusqu'en 1988. Avec cette formule simplifiée on peut retrouver le tableau qui apparaissait sur l'agenda FSE jusqu'en 1989.
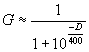
où D est la différence de points Elo entre le joueur et son adversaire.
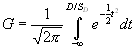
où ![]()
Où K est le coefficient de développement du joueur, et R le résultat (0, 0.5 ou 1).
Que vous choisissiez la variante a)
ou b) j'appellerai maintenant cette fonction fw(D,R),
La Performance Exacte
Qu'est-ce que c'est une performance ?
C'est le niveau d'un joueur, pour lequel il est statistiquement le plus probable d'obtenir ces résultats.
C'est donc le joueur, qui, en obtenant ces mêmes résultats contre ces mêmes joueurs, ne gagne et ne perd pas de points Elo (principe de stabilité du système).
On peut mettre cela en équation et ça donne:
Disons maintenant que chaque D est la différence entre son propre Elo X et l'Elo de l'adversaire E:
= fw(X-E1,R1) + fw(X-E2,R2) + … + fw(X-En,Rn)
X est donc la performance recherchée.
Pour un X donné, nous savons calculer le gain total. Appelons maintenant
cette fonction gain(x).
Maintenant, qu'on utilise à la place de gain(x) la formule a) ou b), il n'est pas possible de trouver une solution analytique é cette équation (de trouver ainsi la fonction inverse). Si quelqu'un parmi vous y arrive, qu'il me le fasse savoir !
Cela explique peut-être que, pendant toutes ces années, on ait utilisé la formule simplifiée de la performance (basée sur la moyenne des Elo).
Ceci dit, aujourd'hui l'informatique est largement domestiquée et, à défaut d'une solution analytique, on peut facilement fournir une solution numérique.
Ce n'est pas difficile, car lorsque "x" croît, "gain(x)" croît également. Il suffit donc, par itérations successives, d'essayer un "x" jusqu'à ce qu'on soit assez proches du "x" qui donne un "gain" = 0.
J'ai procédé ainsi (il existe probablement un méthode avec une convergence plus rapide) :
x = perfC; // performance "classique"
précalculée, c'est un bon départ pour les itérations
pas = eloMax - eloMin;
while (pas > 0.024) { // ça
dépend de la précision que vous voulez obtenir
gain = gain(x) // la fonction "gain"
est celle décrite plus haut
if (gain == 0) break;
pas = pas / 1.99;
if (gain > 0) x = x + pas;
else x = x - pas;
} // x contient maintenant la performance
"exacte"
Rapido calcule
également les performances exactes.